数据表示

存储器

存储器分为主存和辅存，CPU能直接访问主存，主存储器的工作方式是按照存储单元的地址进行存取，这种存取方式称为按地址存取方式。

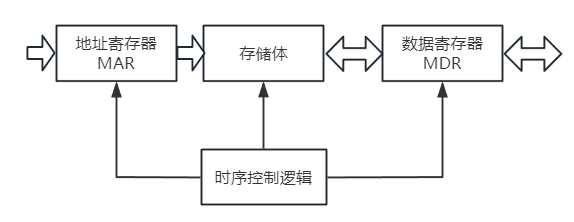
存储体由许多存储单元构成，每个存储单元包含若干存储元件，每个存储元件存储一位（bit）二进制代码“0”或“1”。因此存储单元可存储一串二进制代码，称这串代码为存储字，称这串代码的位数为存储字长，存储字长可以是1字节（B，8bit）或是字节的偶数倍。

主存容量是指主存储器所能存储信息的最大容量，统筹以字节来衡量，也可用字数×字长（如512K×16位）来表示存储容量。其中MAR的位数反映存储单元的个数，并能体现出可寻址范围的最大值。

例如，MAR为16位，表示$2^{16}$=65536，即此存储体内有65536个存储单元（可称为64K内存，1K=1024），若MDR为32位，表示存储容量为64K×32位。

1Byte=8bit，Byte是最小的计量单位，bit是最小的存储单位。在描述存储容量、文件大小时，K、M、G、T通常用2的幂次表示，如1Kb=$2^{10}$b；在描述速率、频率（CPU主频）时，k、M、G、T通常用10的幂次表示，如1kb/s=$10^3$b/s。

进制与数据表示

一个r进制数（$K_nK_{n-1}···K_0K_{-1}K{_-2}$）的数值可以表示为：

$$K_nr^n+K_{n-1}r^{n-1}+···+K_0r^0+K_{-1}r^{-1}+···+K_{-m}r^{-m}=\displaystyle\sum_{i=n}^{-m}K_ir^i$$

式中r是基数，$r^i$是第$i$位的位权，$K_i=0,1,···r-1$。

将任意进制数的各位数码与他们的权值相乘，再把乘积相加，就得到了十进制数$(11011.1)_2=1×2^4+1×2^3+0×2^2+1×2^1+1×2^0+1×2^{-1}$=27.5。

十进制数转换为任意进制数，常采用基数乘除法，对数的整数部分采用除基取余法，对数的小数部分采用乘基取整法，最后将两部分拼接起来。

定点小数（纯小数）的原码：$[x]_原=\begin{cases}x &\text{1>x≥0}\\1-x=1+|x| &\text{0≥x>-1}\\\end{cases}$（$[x]_原是原码机器数，x是真值$），即最高位符号位正数为0，负数为1。

定点整数（纯整数）的原码：$[x]_原=\begin{cases}0,x &2^n\text{>x≥0}\\2^n-x=2^n+|x|&\text{0≥x>-}2^n\end{cases}$（x是真值，n是整数位数），最高位符号位正数为0，负数为1。

补码表示法：

$$\text{纯小数}\quad[x]_补=\begin{cases}x &\text{1>x≥0}\\2+x=2-|x| &\text{0>x≥-1}\end{cases}\text{ (mod 2)} \\\\ \text{纯整数}\quad[x]_补=\begin{cases}x &\text{$2^n$>x≥0}\\2^{n+1}+x=2^{n+1}-|x| &\text{0>x≥-$2^n$}\end{cases}\text{ (mod $2^{n+1})$}$$

即符号位不变，其他按位取反再+1。

补码表示法中的加减运算可统一采用加法操作来实现。

浮点数：$N=(-1)^s×M×R^E$，由数符、尾数和阶码三部分组成。